ひし形 - 面積、周囲長の計算
Rhombus Area Calculator
ひし形面積計算機(Rhombus)
菱形の公式(Rhombus)
Area - エリア = (d₁ × d₂) / 2
Perimeter - 周囲 = 4 × √[(d₁/2)² + (d₂/2)²]
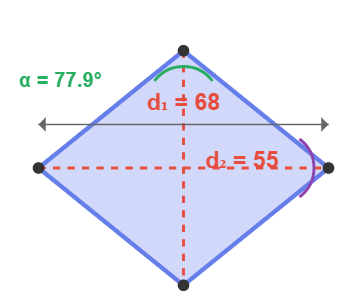
Vertex Angles - 頂点角度: α = 2 × arctan(d₂/d₁), β = 180° - α
ひし形面積計算機(Rhombus)
菱形の公式(Rhombus)
Area - エリア = (d₁ × d₂) / 2
Perimeter - 周囲 = 4 × √[(d₁/2)² + (d₂/2)²]
Vertex Angles - 頂点角度: α = 2 × arctan(d₂/d₁), β = 180° - α
ひし形 - 面積、周囲長の計算
ひし形の面積計算機
この計算機は、両方の対角線（d₁とd₂）を入力としてひし形の面積を計算します。
• 計算式：面積 = (d₁ × d₂) / 2
• 戻り値：ひし形の面積（平方単位）。
• キーワード：ひし形の面積計算機、ひし形の面積の計算式、対角線を使用したひし形の面積の計算。
________________________________________
ひし形の周囲長計算機
この計算機は、対角線の長さを使用してひし形の周囲長を計算します。
• 計算式：周囲長 = 4 × √[(d₁/2)² + (d₂/2)²]
• 戻り値：周囲長（線形単位）。
• キーワード：ひし形の周囲長計算機、ひし形の周囲長の計算、ひし形の辺の長さの計算機。
________________________________________
ひし形の角度計算機
このツールは、対角線を使用してひし形の頂角も計算します。
• 鋭角 (α): α = 2 × arctan(d₂ / d₁)
• 鈍角 (β): β = 180° – α
• 戻り値: α (鋭角) と β (鈍角) の値。
• キーワード: ひし形の角度計算、ひし形の鋭角、ひし形の鈍角、ひし形の形状計算。
________________________________________
ひし形の辺の長さ計算
この計算ツールは、対角線を用いてひし形の辺の長さを計算します。
• 計算式: 辺 = √[(d₂/2)² + (d₂/2)²]
• 戻り値: ひし形の辺の長さ。
• キーワード: ひし形の辺の長さ計算、対角線からひし形の辺を求める、ひし形の特性計算。
________________________________________
ひし形計算のための複数の入力オプション
• 対角線1と対角線2を入力として受け付けます。
• ユーザーは両方の対角線を入力して、以下の計算を行います。
o 面積
o 周囲長
o 辺の長さ
o 角度（鋭角と鈍角）
• キーワード：ひし形計算ツール、ひし形の対角線計算ツール、ひし形特性計算ツール、オンライン幾何学計算ツール。
________________________________________
数式参照セクション
ひし形幾何学の参照を含む組み込み数式セクション：
• 面積 = (d₁ × d₂) / 2
• 周囲長 = 4 × √[(d₁/2)² + (d₂/2)²]
• 角度：α = 2 × arctan(d₂/d₁), β = 180° – α
• キーワード：ひし形の数式、ひし形の幾何学、数式計算ツール。
________________________________________
面積、周囲長、辺の長さ、対角線の角度を求める無料オンラインひし形計算機。インタラクティブなひし形図、幾何学の公式、モバイルフレンドリーなデザインが含まれています。学生、教師、専門家に最適です
